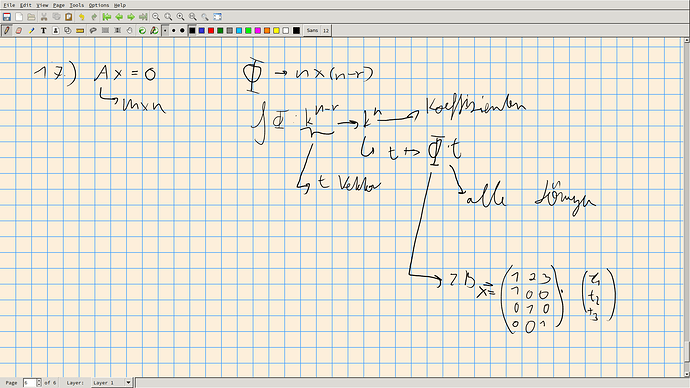
Was ist eine Fundamentalmatrix und welche Idee verbirgt sich dahinter?
Ich habe bisher Analysis gemacht.
Werde morgen Laag machen  Dann kann ich dir mehr sage.
Dann kann ich dir mehr sage.
Merkwuerdig… im LAG skript vom Vorjahr steht auch nischt…
Eine Fundamentalmatrix wird auf dem Aufgabenblatt als die Matrix definiert, die einem (oder mehr) frei wählbaren Parameter die Vielfachen zuweist, sodass die Multiplikation eines homogenen LGS (in Matrixschreibweise, duh) mit dieser (und dem Parameter) eine Nullmatrix (nur mit Nullen gefüllt) ergibt.
Nuh. Das klingt (ohne nähere überlegung) erscht Mal nach einer Lösung eines homogenen LGS, wie wir sie in der Vorlesung am Donnerstag vor zwei Wochen für normale LGS aufgeschrieben haben…
Was anderes sollte das auch nicht sein ^.^
Auf dem Aufgabenblatt steht ja, dass die Lösung eines homogenen LGS und die Erstellung einer Fundamentalmatrix quasi das selbe sind.
Und wo ist dann genau der unterschied? Also wie sieht ne fundermentalmatrix beispielsweise aus? Bei der 2. Matrix von 17. ii hab ich:
(1 2 3)
(0 1 2) dabei is x1,x3=t und x2=-2t
Aber wie gebe ich jetz dazu die fundamentalmatrix an?
Jo. Also zuers: denkt Mal darüber nach, was passiert wenn r=0.
Dann hat das LGS nur eine Lösung: die triviale.
Andernfalls gibst du einfach das an, was wir in der Vorlesung hatten. Also ne Mischung aus dem Rest und der Einheitsmatrix.
(1 0) (-1)
(0 1) +t * (2 ) das is ja keine fundamentalmatrix oder?
Oder ist es einfach:
(1 0 -1)
(0 1 2)