Nummerierung für die Mandelstam-Variablen

[Bengt]

Für die Berechnung der Mandelstam-Variablen bzw. der Bestimmung des Kanal-Types eines Feynman Diagramms muss man die ein- und ausgehenden Teilchen durchnummerieren. Für einen 2 -> 2 Prozess nutzt man 1 und 2 für die eingehenden, 3 und 4 für die ausgehenden Teilchen. Soweit habe ich es denke verstanden.
Wenn ich mir jetzt die Vorlesung 9 (Folie 15, 16, 17), meine Mitschriften aus der 5. Übung und den Wikipedia Artikel anschaue sieht es fast so aus, als wäre die Nummerierung willkürlich.
Wikipedia Nummeriert mit jeweils 1 und 3 oben für ein und ausgehend (bzw links und rechts) und 2 und 4 unten.
In der Übung sind konsequent 1 und 4 oben für ein und ausgehend (bzw links und rechts) und 2 und 3 unten.
Und in der Vorlesung tauchen 2 verschiedene Nummerierungen auf. Direkt bei der Einführung ist 2 und 4 oben für ein und ausgehend (bzw links und rechts) und 1 und 3 unten (also horizontal gespiegelt). Beim Beispiel für den u-Kanal 2 Folien weiter ist dann 3 und 2 oben für ein und ausgehend (bzw links und rechts) und 1 und 4 unten.
Mein Problem ist, dass wenn ich bei der Nummerierung nicht konsistent bin, dann kann ja bei meinem Kanal-Typ alles möglich herauskommen oder nicht?
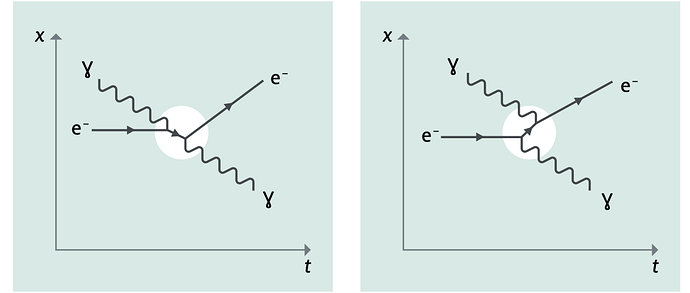
ZB. Die Compton-Streuung aus Teilchenwelt 1

Ich weis aus der Vorlesung, dass das linke Diagramm ein s-kanal ist und das rechte ein u-kanal.
Für den s-Kanal ist dabei nur wichtig, dass links die 1 und 2 für die einkommenden Teilchen stehen und rechts die 3 und 4 für die ausgehenden. Dh. unabhängig davon wie ich nummeriere, solange die eingehenden 1 und 2 sind und die ausgehenden 3 und 4, ist ein s-kanal Diagramm immer ein s-kanal Diagramm.
Das Problem für mich tritt beim rechten Diagramm auf. Wenn ich das richtig verstanden habe dann ist am unteren Vertex das Elektron eingehend und das Photon ausgehend und am oberen umgekehrt (Emission -> Absorption). Dh links stehen auf jedenfall 1 und 2 und recht 3 und 4. Wenn ich jetzt für die Mandelstam Variable q_{\mu}q^{\mu} bestimmen möchte, schaue ich mir einen der Vertices genauer an. Wenn ich den unteren betrachte habe ich q_{\mu}q^{\mu} = ({p_{e^-}}^{\mu}- {p_{\gamma}}^{\mu})^2 oder? Wenn ich jetzt alle Nummerierungsmethoden von oben durchteste, dann bekomme ich laut der Vorlesung q_{\mu}q^{\mu} = ({p_{1}^{\mu}}- {p_{3}}^{\mu})^2 (t-Kanal), laut Wikipedia q_{\mu}q^{\mu} = ({p_{2}}^{\mu}- {p_{4}}^{\mu})^2 (auch t-Kanal) und laut der Übung q_{\mu}q^{\mu} = ({p_{2}}^{\mu}- {p_{3}}^{\mu})^2 (u-Kanal). Demnach wäre lediglich die Nummerierung der Übung richtig. Da ich aber am ehesten der Vorlesung vertrauen würde, bin ich mir sehr sicher, dass ich bei dem ganzen irgendwas nicht richtig verstanden habe. Gibt es beim Nummerieren eine weitere Regel außer 1,2 eingehend; 3,4 ausgehend?

[Bengt]

In der Folie der Vorlesung steht auch noch, dass ähnliche Teilchen die Zahlen wie folgt zugeordnet werden 1<->3 und 2<->4. Damit wäre laut Vorlesung der Impulsübertrag p_{\mu}p^{\mu}=(p_{1}-p_{4})^2, was dem u-Kanal entspricht also alles richtig. Ich hatte einen Denkfehler.
Die beiden relevanten Regeln sind also:

• 1,2 für die eingehenden Teilchen; 3,4 für die ausgehenden
• die ähnlichen (gleichen Teilchen) jeweils gerade und ungerade zugeordnet (1,3 und 2,4)

[mkobel]

Lieber Bengt,
Korrekt, das ist die Antwort. Es ist wichtig, dass gleiche (oder ähnliche) ein- und ausfliegende Teilchen jeweils (1,3) und (2,4) zugeordnet werden. Ob bei den einfliegenden Teilchen 1 oben und 2 unten ist, oder umgekehrt, ist völlig egal. Denn es ist ja auch egal, welches Teilchen ich oben, und welches ich unten zeichne. Es kann gut sein, dass ich das in der Vorlesung / Übung mal so, mal anders gemacht habe. Da Energieerhaltung gilt, kommt immer dasselbe raus, denn bei t-Kanal ist t=(p_1^µ - p_3^µ)^2 = (p_2^µ - p_4^µ)^2.
Manchmal, wie bei e^+e^-\to \gamma\gamma muss man sogar beide Möglichkeiten addieren, d.h. die Photonen mit 3 (oben) und 4 (unten) **plus ** 4 (oben) und 3 (unten) beziehungsweise bei \gamma\gamma \to e^+e^- die Photonen mit 1 (oben) und 2 (unten) **plus ** 2 (oben) und 1 (unten) bezeichnen, so dass ein t-Kanal und ein u-Kanal entsteht. Denn ich kann mir ja im letzteren Fall (zB im SP-System) festlegen, dass Photon 1 in +z-Richtung fliegt und Photon 2 in -z Richtung. Wenn ich nur eines der Diagramme betrachten würde, ergäbe sich zB bei e^+ als „3“ , dass in diesem t-Kanal das Positron auch bevorzugt in +z-Richtung fliegt, da es von dem Photon 1 abgestrahlt wird. Ich brauche also auch das u-Kanal Diagramm, in dem das Positron von Photon 2 abgestrahlt wird.

herzliche Grüße
Michael Kobel