Es steht geschrieben
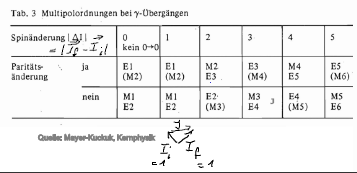
Aber S=1, L=1 koppeln z.b. zu 0, 1, 2
Hmm, in der Tat tritt das nicht auf. Es gibt offensichtlich aus Paritätsgründen keine M0 Übergänge, die einem Photon 1^- plus Drehimpuls 1^- gekoppelt zu J^P=0^- entsprechen würden. E0 Übergänge mit J^P=0^+ würde die Parität erlauben, gibt es aber nicht. (Warum?? Ich weiß es grade leider nicht. Kannst Du suchen?). Daher sind 0->0 Übergänge verboten. Siehe unten
Bei 1^- \to 1^- muss Bahndrehimpuls L=1 dazwischen sein. Das ist ein M1 Übergang (Kopplung von Photon-Spin und Bahndrehimpuls zu J^P=1^+ oder ein E2 Übergang (Kopplung zu J^P=2^+).
Sorry, das Verstehe ich nicht.
Sollte es nicht zu 0^+ koppeln?
Diese Paritaetsgeschichten kommen doch aus den uebergangsopertatoren, die es fuer 0-momente nicht gibt. Bezieht sich die Argumentation auf:
E0 gibts nicht, da hier coulomb eichung genommen wird und das skalarpotential \phi = 0 ist. (glaube ich irgendwo gelesen zu haben)
Eben, bei 1^- \to 1^- könnte das Photon prinzipiell mit einem Bahndrehimpuls zu 0^+ koppeln. Das wäre dann ein E0 Übergang (nach definition von E und M). Aber E0 gibt’s nicht, aus Gründen die ich nicht mehr weiß. Es kann gut sein, dass man das aus der Eichfreiheit sieht.
Die Definition ist, dass EJ wie folgt läuft
0^+, 1^-, 2^+, 3^-, 4^+ usw
und dass MJ grade jeweils die andere Parität hat.
Ok ich las gerade nach, dass das Stralungsfeld aufgrund der Transversalitaet kein l=0 haben kann.
Desswegen erst dipol strahlung mit l=1.
Es scheint auch irrefuehernd zu sein den Spin des Photons mitzubetrachten, da das klassische Strahlungsfeld einfach einen bestimmten (bahn) Drehimpuls hat. (laut Mayer-Kuckuk)
Hmm. Naja, vlt ist das richtig aufklamuesert wenn man Quantenfeldtheorie benutzt, aber ich gebe mich gern mit klassischem Strahlungsfeldern zufrieden.
Hmm after some thought: das klassische \ell scheint schon der gesamtdrehimpuls zu sein, amen.
Die Sache mit J>0 scheint wohl durch die fehlende m=0 einstellung des Photonenspins bedingt zu sein.
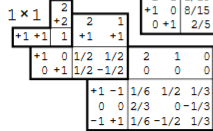
Ich zweifle, dass das die richtige Erklärung ist. Der Clebsch-Gordan Koeffizient erlaubt durchaus (1,+1)+(1,-1)->(0,0). Man braucht also kein (1,0) um (0,0) zu erzeugen:
Hilft das vielleicht weiter (Quelle www.ipen.br)?
nunja, das ist wieder das klassische Strahlungsfeld…
Bei Gelegenheit kann ich mich ja mal mit Quantenoptik beschäftigen 
oder wir fragen mal nen Theoretiker. Soll ich Dominik Stöckinger fragen?
Klassisch isses jedenfalls nun klar: Der Übergangsoperator für E0 ist konstant und damit ist die Übergangsrate null, weil die Zustände aufeinander senkrecht stehen.
1 „Gefällt mir“
es scheint auch komplizierter zu sein, da man die normalmodenzerlegung in der QFT auf unterschiedliche weise machen kann,
Mit den Kugeflaechenfkt kommt dann evtl genau der Umstand raus, dass \ell=0 nicht vorhanden ist.
Jo das ist eine gute Idee :).
Ich denke aber nicht, dass der uebergangsoperator Konstant ist. Im Mayer-Kuckuk wurde gezeigt, dass \nabla \cdot E,B = 0 die \ell=0 verbietet (klassisch).
Instruktiv waehre es warscheinlich, sich mal den Kanonischen Drehimpulsoperator anzuschauen.
Oha: http://dx.doi.org/10.1103/PhysRevA.73.013805
Es scheint beim Photon nicht sinnvoll zu sein, in Bahndrehimpuls und Spin zu zerlegen, weil die Operatoren gar keine Drehimpulsalgebra erfuellen.
Siehe auch;
geklaut aus: https://link.springer.com/chapter/10.1007/978-3-642-17410-0_17
Dochdoch, der klassische E1-Operator ist e\vec{r} (siehe Vorlesung), der E0- Operator ist e und damit konstant.
1 „Gefällt mir“
Nunja, da fehlt mir die Theorie 
.
Vlt ist es die Tatsache, dass e nur an das skalarpotential koppelt, welches wir rausgeeicht haben :).
So, ich habe nochmal drüber nachgedacht, wie man das anschaulich mit Drehimpulskopplungen verstehen kann und bin auf folgende Erklärung gekommen. Sie mag naiv sein, aber ich finde sie schön (was aber nicht heißt dass sie richtig ist 
). Immerhin kommt wirklich raus, dass |0,0> nicht geht, weil das Photon niemals Spin |1,0> haben kann. Was mir dazu bisher fehlte war die Erkenntnis, dass ausschließlich L=|L,0> beiträgt, weil \vec{L} \perp \vec{S}. Wenn man das annimmt, ist alles klar:
1 „Gefällt mir“
klingt zumindest plausibel
1 „Gefällt mir“