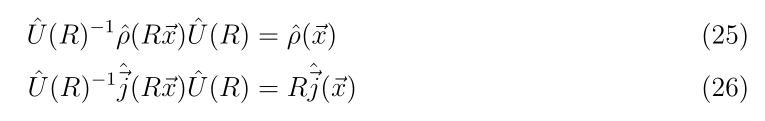Nachdem ich mich erleuchtet waehnte und ich dann aber doch nochmal nachdenken musste, teile ich hier meine (eventuell vermeindlichen) Erkenntnisse.
Sei U eine Rotations-Transformation.
Ein gewoehnlicher Operator A trift eine Aussage ueber das System (als „Messaparate“). Wenn ich nun mein System drehe und meinen Messaparat gleich mit so sollte gelten
und wie wir seit jeher wissen kann man folgern: A' = UAU^{-1}.
Die Aussage die von Feldoperatoren getroffen wird ist nun etwas anders, wenn sie sich auf den Raum bezieht. Man nehme die Teilchendichte \hat{\rho}(\vec{x}) . Dann ist die Aussage die man ueber einen Zustand treffen kann: \langle\psi |\hat{\rho}(\vec{x})| \psi\rangle =\text{"Die Teilchendichte des Zustands am Ort } \vec{x}\text{ ist } \langle\psi |\hat{\rho}(\vec{x})| \psi\rangle\text{"}.
Transformiert man nun aber das System, so „drehen“ sich die Zustaende, aber die Raumbezogene aussage steckt im Argument (man denke sich den Operator als Mannigfaltigkeit von Operatoren indiziert durch \vec{x}). Desshalb bleibt hier der Operator der Gleiche und das Argument „dreht mit“.
Damit ergibt sich die Transformationsregel (oder Vorderung) aus dem Skript. (Aus Faulheit als Bild.)
Wer Lust und Laune hat, kann dieses Verhalten mal an
ausprobieren (\{|\nu\rangle\} sei beliebige Einteilchenbasis). Es kommt wirklich raus!